La tarification des produits a un impact énorme sur le chiffre d'affaires et la marge bénéficiaire. Il ressort toutefois d'une étude qu’une meilleure estimation du coût n’entraîne pas forcément une hausse du bénéfice.
Deux méthodes sont couramment utilisées pour fixer le prix d’un produit industriel. Soit on se base sur les prix des concurrents, soit on calcule le coût et on y ajoute une marge bénéficiaire. Cette dernière, la méthode cost-plus, est de loin la plus répandue dans l’industrie. En effet, de nombreux produits industriels sont spécifiques au client et le prix du concurrent n’est pas public.
Incertitudes lors de la tarification
Avec la méthode cost-plus, le prix dépend fortement de l’estimation du coût. Dans la pratique, il n’est pas aisé d'évaluer le coût à l'avance. Le calcul du coût réel basé sur les temps de production enregistrés révèle presque toujours des différences. Le prix effectivement payé pour les matériaux et la consommation de matériaux, peuvent également s’éloigner des coûts initialement estimés. Généralement, il est encore plus délicat d’établir la marge. D’ordinaire, on n’applique pas une marge fixe, celle-ci dépendant des conditions de marché : qui sont les concurrents présumés, quelle est la sensibilité au prix du client, dans quelle mesure l’acheteur peine-t-il à réaliser son chiffre d'affaires, etc.
Vu ces incertitudes, il est possible que, pour deux devis similaires, le prix varie selon le moment où ceux-ci sont établis. La concurrence faisant évidemment face aux mêmes incertitudes, ses prix peuvent également osciller.
Le client va profiter de cette dispersion des prix et choisir l’offre la moins chère. À première vue, le client semble sortir gagnant de ce jeu et le fournisseur perdant. « Les offres dont nous sous-estimons le coût trouvent preneur, tandis que celles dont l’estimation est correcte sont remportées par la concurrence. » Ce problème est souvent évoqué.
On pourrait penser qu’une meilleure estimation des coûts serait la solution. Si on connaît plus précisément les coûts, on pourra mieux fixer le prix et l’entreprise sera plus rentable. Cela semble logique, mais est-ce bien le cas ? Un meilleur calcul du prix de revient génère-t-il effectivement plus de bénéfice ?
Impact sur la probabilité de succès de l’offre
Réfléchissons sur l’impact de la dispersion des prix sur le bénéfice d’une entreprise. Supposons qu’un client demande un devis à trois entreprises (A, B et C). Pour établir clairement l’impact de la dispersion des prix, considérons que les produits et services des trois concurrents sont équivalents. Le choix du client repose donc uniquement sur le prix. Par ailleurs, la structure des coûts est similaire chez les trois concurrents. Le prix moyen proposé est donc le même. La variation de prix entre les trois entreprises dérive donc uniquement des incertitudes lors du calcul du prix de revient.
Dans notre exemple, nous allons partir du principe que les incertitudes peuvent faire varier le prix de chaque entreprise de +/-10%. Pour un prix moyen de 100 euros, le plus bas prix proposé sera donc de 90 euros et le plus élevé de 110 euros. Comme les trois entreprises sont équivalentes à tous les niveaux, chacune a autant de chances de proposer le prix le plus bas et donc de décrocher la commande. La probabilité de succès d’une offre est donc d’un tiers (33,3%).
L’entreprise A est toutefois insatisfaite de la situation. Elle imagine une méthode ingénieuse de calcul du prix de revient qui élimine toute incertitude. Cette méthode annule la dispersion du prix. Le prix est donc toujours de 100 euros. Quelle est alors la probabilité de succès d’une offre ?
Si l’entreprise A veut décrocher la commande, elle doit proposer le prix le plus bas. Le prix des concurrents B et C doit donc se situer dans une fourchette de 100 à 110 euros. La probabilité que le prix de l’entreprise B se situe dans la moitié supérieure de la fourchette de prix est de 50%. Il en va évidemment de même pour l’entreprise C. La probabilité que les concurrents se trouvent tous les deux dans la fourchette supérieure est donc de 50% x 50% = 25%. La probabilité de succès d’une offre (et donc la part de marché) va passer de 33,3% à 25% si l’entreprise A améliore son calcul du prix de revient !
Et si l’entreprise A avait fait l’inverse, en consacrant moins d’énergie au calcul du prix de revient, le rendant ainsi plus approximatif ? La figure 1 répond à cette question. L’axe des abscisses représente la dispersion relative des prix, qui est le rapport entre la dispersion du prix de l’entreprise A et la dispersion chez les concurrents. Pour une dispersion des prix relative de 1, toutes les entreprises présentent la même dispersion du prix et la probabilité de succès est de 33,3%. Pour une dispersion relative des prix nulle, le prix ne varie plus dans l’entreprise A et sa probabilité de succès est de 25%. Pour une dispersion relative de 2, le prix de l’entreprise A varie autant que chez les concurrents. Dans ce cas, la probabilité de succès des offres grimpe à plus de 40%.
La figure montre également l’impact du nombre de concurrents sur la probabilité de succès pour une demande d’offre. Si le client ne demande une offre qu’à une autre entreprise, la probabilité de succès est toujours est de 50% et ne dépend plus de la dispersion relative du prix. Plus le client demande d’offres, plus la probabilité de succès baisse lorsqu’on affine le calcul du prix de revient. Avec quatre concurrents, la probabilité de succès d’une offre passe ainsi de 20% (= une chance sur cinq) à 6,25% (= 50% x 50% x 50% x 50%), pour un calcul parfait du prix de revient. Notez que dans notre exemple, le nombre de concurrents dépend du nombre d’offres demandées par le client et non du nombre total de concurrents de l’entreprise sur le marché.
Impact sur le chiffre d'affaires
Le raisonnement ci-dessus donne la probabilité de succès des offres, et ainsi la part de marché en unités vendues. Si la dispersion des prix s'accroît, la probabilité de succès va également augmenter, mais cela découle du fait que davantage d’offres sont soumises à un prix inférieur. La demande accentue aussi l’impact de la dispersion des prix sur le chiffre d'affaires, et en fin de compte sur le bénéfice.
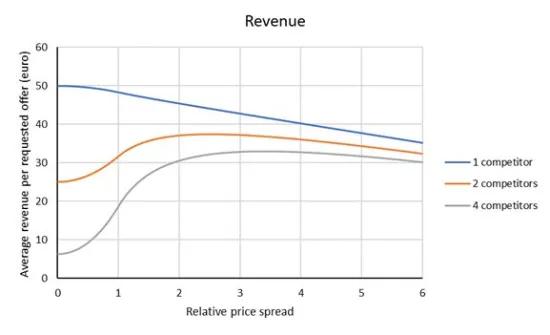
Jetons d'abord un œil au chiffre d'affaires. Pour évaluer l’impact de la dispersion des prix sur le chiffre d'affaires, nous avons réalisé quelques calculs, dont les résultats sont présentés dans la figure 2.
Les calculs et la figure 2 permettent de tirer les conclusions suivantes :
- Si le client ne demande que deux offres (l’entreprise A n'a qu’un concurrent), le chiffre d'affaires augmente légèrement de 3,5% avec un calcul parfait. Dans la pratique, l’impact sera bien moins important, car les calculs parfaits ne sont pas possibles.
- Si le client demande une offre à trois entreprises (l’entreprise A a deux concurrents), le chiffre d'affaires baisse de 21% avec un calcul parfait. Cette baisse s'amplifie encore lorsque le client demande une offre à plus d’entreprises.
- Lorsque le calcul du prix de revient devient plus approximatif que la dispersion des prix de la concurrence (dispersion relative des prix supérieure à 1), le chiffre d'affaires augmente d'abord, puis atteint un maximum pour ensuite redescendre lentement. Dans notre exemple avec deux concurrents, le maximum est atteint lorsqu’on fait passer la dispersion à +/-25% (dispersion relative des prix de 2,5 par rapport à la fourchette de +/-10%).
Impact sur le bénéfice
Maintenant que nous connaissons la probabilité de succès de l’offre et le chiffre d'affaires, nous sommes en mesure de déterminer le bénéfice. Il faut ici opérer une distinction entre les coûts variables et les coûts fixes. Le coût variable total (p. ex. coût des matériaux) dépend du volume de production. Il est donc proportionnel à la probabilité de succès des offres. Le coût fixe dépend, dans certaines limites, du volume de production.
La précision du calcul du prix de revient influe directement sur la probabilité de succès de l’offre, et donc sur le chiffre d'affaires total et le coût variable total, mais pas sur le coût fixe. Pour connaître l’impact sur le bénéfice, il suffit donc de calculer la différence entre le chiffre d'affaires et le coût variable total : la contribution. Plus la contribution est élevée, plus le bénéfice est élevé.
Cas le plus simple : le client demande une offre à deux entreprises. Dans ce cas spécial, la probabilité de succès ne dépend pas de la dispersion des prix, elle est toujours de 50%. Dès lors, le volume et donc aussi le coût variable total sont constants. Cela signifie que le bénéfice ne dépend que du chiffre d'affaires. Le bénéfice va donc se comporter comme le chiffre d'affaires et enregistrer une légère hausse lorsqu’on améliore le calcul du prix de revient.
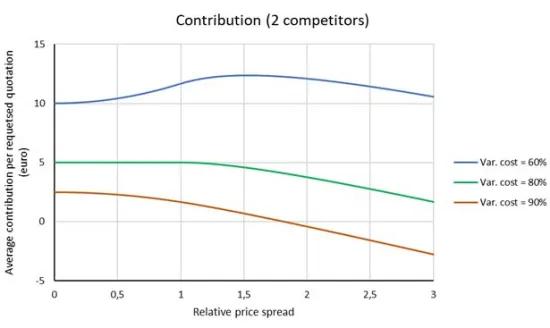
La figure 3 montre les résultats de notre calcul pour les différents coûts variables lorsque le client demande trois offres (l’entreprise A a donc deux concurrents).
Le graphique ci-dessus et les calculs associés permettent une fois encore de tirer des conclusions surprenantes :
- Le comportement de la contribution et du bénéfice dépend de la part des coûts variables. Lorsque la part du coût variable par rapport au prix moyen est très élevée, l'affinement du calcul du prix de revient entraîne une hausse du bénéfice.
- Lorsque la part du coût variable est relativement faible, l'affinement du calcul du prix de revient entraîne une baisse du bénéfice. Dans ce cas, il est même indiqué d’être moins précis dans le calcul du prix de revient. Dans notre exemple, le bénéfice pour une part du coût variable de 60% atteint un maximum lorsque l’incertitude du calcul du prix passe de +/-10% à +/-15%.
- Pour une part donnée du coût variable, l'affinement du calcul du prix de revient n'a aucun effet, mais le bénéfice décroît lorsque le calcul du prix de revient devient moins précis. Dans notre exemple, ce point de basculement correspond à un coût variable de 80 euros (80% du prix moyen), soit une contribution de 20 euros par produit. Notez que la contribution de 20 euros correspond à la fourchette de prix sur le marché (différence entre le prix le plus haut et le prix le plus bas : 110 - 90 = 20 euros). Ce n'est pas un hasard. De manière générale, on peut dire que ce point de basculement (avec deux concurrents) se présente lorsque la contribution d’un produit est égale à la fourchette de prix du marché.
Lorsque la contribution d’une offre est supérieure à la fourchette de prix sur le marché, l'affinement du calcul du prix de revient impacte donc le bénéfice. Dans la pratique, c’est souvent le cas. Ce constat nous amène au paradoxe du coût : l'affinement du calcul du prix de revient peut entraîner une baisse du bénéfice !
Implications pratiques
La précision du processus d'estimation du coût est régulièrement évaluée en comparant le calcul du coût prévisionnel au calcul du coût réel. Ce processus a donc des conséquences considérables.
D'abord, il peut générer des frictions et des discussions interminables entre le management et les collaborateurs en production. Perd-on trop de temps sur une commande à cause d’une sous-estimation du coût prévisionnel ou des performances des collaborateurs en production ?
Ensuite, les personnes chargées du calcul des coûts vont passer beaucoup de temps à estimer les coûts pour éviter les récriminations. Elles vont ainsi se surcharger et le client risque d'attendre longtemps pour obtenir une offre.
Étant donné que de nombreux clients sont très attentifs à la rapidité du délai de réponse, il vaut souvent mieux viser la rapidité du processus d’offre que sa précision. La rapidité de la formulation de l’offre peut souvent augmenter la probabilité de succès. Comme nous l'avons expliqué, les éventuelles imprécisions ne sont peut-être pas aussi préjudiciables qu’on pourrait le penser.
